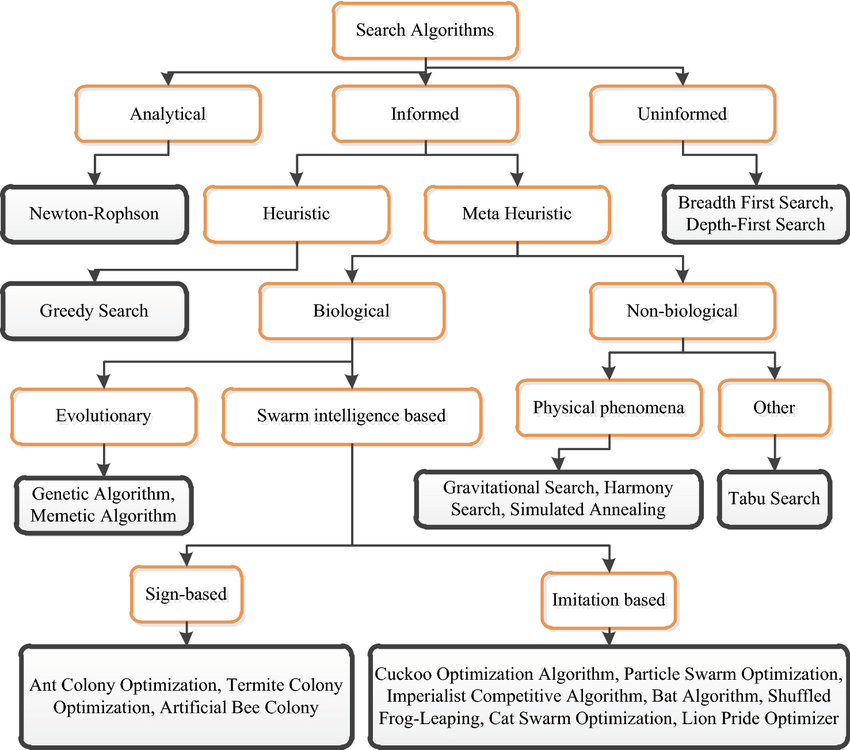
Solving optimization problems in power systems is inherently challenging due to their vast scale, intricate complexity, extensive geographical coverage, and susceptibility to various unforeseen events. Consequently, it becomes imperative to employ highly efficient optimization methods that can effectively simplify the problem formulation and implementation. This article provides a comprehensive overview of key mathematical optimization techniques and artificial intelligence (AI) approaches commonly employed in power optimization problems. Furthermore, the article explores the application of hybrid AI techniques in this field.
Introduction
Over the years, mathematical optimization methods have been extensively utilized for power systems planning, operation, and control problems. These methods involve deriving mathematical formulations of real-world problems based on certain assumptions. However, solving large-scale power system problems is far from simple, even with these assumptions in place. Power systems are characterized by their vast size, complexity, and wide geographical distribution, resulting in numerous uncertainties.
Furthermore, the deregulation of power utilities in recent times has introduced new challenges to existing problems. While it is desirable to find globally optimum solutions for power system problems, traditional mathematical optimization techniques often yield only locally optimal solutions. This inherent limitation makes it challenging to effectively address many power system problems using strict mathematical formulations alone.
To overcome these limitations, artificial intelligence (AI) techniques have emerged as complementary tools to mathematical approaches in power systems. AI techniques, such as expert systems (ES), artificial neural networks (ANN), genetic algorithms (GA), and fuzzy logic, promise global or near-optimal solutions. The origins of AI can be traced back to 1958, and since then, various optimization techniques have been applied to solve power system problems, leading to a substantial body of published research in this field since the 1950s.
Mathematical Optimization Methods
Mathematical optimization methods involve the use of mathematical models to minimize undesirable factors (e.g., cost, energy loss, errors) or maximize desirable factors (e.g., profit, quality, efficiency), while considering certain constraints. These methods offer several advantages:
- Rigorous Optimality: Certain algorithms provide mathematically rigorous optimality, ensuring the solutions obtained are truly optimal.
- Sparsity Techniques: Problems can be formulated to leverage sparsity techniques that are suitable for large-scale power systems. This allows for efficient and scalable optimization approaches.
- Diverse Mathematical Programming Technologies: A wide range of mature mathematical programming technologies are available. These include linear programming (LP) and interior point (IP) methods, quadratic programming (QP), nonlinear programming (NLP), decomposition techniques, integer and mixed-integer programming, dynamic programming (DP), and more.
The following section provides a brief overview of the important mathematical optimization techniques commonly used in power systems problems:
Linear and Quadratic Programming
Linear and quadratic programming techniques are widely used in solving optimization problems in various domains. When the objective function and constraints are linear, the resulting problem is referred to as a linear programming (LP) problem. LP methods can be broadly categorized into simplex and interior point (IP) methods. Simplex method, as one of the LP methods, is known for its computational efficiency, making it suitable for solving problems with thousands of variables and constraints. However, a drawback of the simplex method is that the number of iterations required grows exponentially with the size of the problem.
To overcome this limitation, interior point methods (IP) can be utilized. Unlike the simplex algorithm, IP methods do not move from one corner point to the next within the constrained region. Instead, they remain within the interior of the region and progressively converge towards the optimal point. Several IP algorithms have been developed and applied to various power system problems, such as economic dispatch, reactive power optimization, and power system optimization.
In addition to linear objectives and linear constraints, LP methods can also be extended to handle problems with a combination of linear and quadratic objective functions. Such problems are referred to as quadratic programming (QP) problems. The QP methods enable the optimization of systems that involve both linear and quadratic terms in the objective function while maintaining linear constraints.
Nonlinear Programming
Nonlinear Programming (NLP) arises when either the objective function or the constraints involved are nonlinear. Unlike Linear Programming (LP), which deals with solving sets of linear equations, NLP involves solving sets of nonlinear equations. In NLP methods, the general approach is to begin with an initial estimate and determine a “descent direction” that leads to a decrease in the objective function for minimization problems.
Numerous NLP methods are available, each with its own definition and step length. The Quasi-Newton method, for instance, aims to construct an approximation of the Hessian matrix and can exhibit robust convergence. However, it requires matrix operations, which can be a drawback. If the coefficients of the Hessian matrix can be obtained analytically, the Newton method can be employed.
Integer and Mixed-Integer Programming
Integer and mixed-integer programming are techniques used to solve optimization problems where some variables can only take integer values, and others can be continuous. In integer programming, all variables are constrained to integer values, while in mixed-integer programming, some variables are allowed to be continuous. These techniques have been widely applied in various areas of power systems, such as optimal reactive power planning, power systems planning, unit commitment, and generation scheduling.
To solve integer programming problems, two main approaches have been used: “branch and bound” and “cutting plane methods.” These mathematical programming techniques have been effective in solving integer problems, enabling the solution of problems with hundreds of variables. The size and complexity of integer and mixed-integer programs that can be practically solved depend on the problem’s structure.
Dynamic Programming
Dynamic Programming (DP) is a problem-solving technique based on the principle of optimality. According to this principle, an optimal policy consists of sub-policies that are also optimal on their own. For instance, let’s consider a problem with n generators, each having s possible output levels. If we were to exhaustively examine all combinations, it would require s*n possibilities. However, using DP, we can examine fewer than n2s2 combinations. DP is an extremely powerful technique when applicable, although it is affected by the curse of dimensionality, as mentioned in. For instance, in the example provided where n equals 100 and s equals 200, the total number of combinations would be n2s2, resulting in 4 X 108 possibilities. DP has found applications in various areas of power systems such as reactive power control, transmission planning, and unit commitment.
Artificial Intelligence Techniques
In addition to the algorithmic approaches discussed earlier, there are certain problems that cannot be fully solved using conventional methods. These problems involve:
- Utilizing knowledge bases to store human knowledge.
- Incorporating operator judgment, especially in practical solutions.
- Leveraging experience accumulated over time.
- Dealing with network uncertainty, load variations, and other similar challenges.
This section provides an overview of various AI techniques, such as Expert Systems (ES), Artificial Neural Networks (ANN), fuzzy systems, Evolutionary Computation (EC), ant colony search, tabu search, and more. These techniques are specifically employed for addressing power systems problems.
Expert System
Expert System (ES) is a knowledge-based or rule-based system that utilizes knowledge and interface procedures to address complex problems requiring human expertise. ES was extensively researched by Feigenbaum et al. in the early 1970s. It offers several advantages, including permanence, consistency, easy transferability or reproduction, and documentation. However, ES suffers from a knowledge bottleneck as it lacks the ability to learn or adapt to new situations.
Applications of ES in the power industry have varied in maturity, ranging from software prototypes to practical systems in use. The field of knowledge engineering has evolved from simplistic rule-based techniques to more advanced approaches such as object-oriented design, qualitative reasoning, verification and validation methods, natural languages, and multi-agent systems.
Over the past two decades, numerous ES applications have been developed to aid in planning, analysis, management, control, and operation of different aspects of power generation, transmission, and distribution systems. Extensive surveys of ES applications in the power system domain have been conducted. and other researchers. These applications encompass diverse areas such as power system planning, alarm processing, fault diagnosis, power system protection, power system restoration, and reactive power/voltage control. A recent survey highlights the wide range of ES applications in various areas of power systems.
Artificial Neural Network
Artificial Neural Networks (ANN) are a type of computational model inspired by the structure and functioning of biological neural networks. The concept of ANN originated from Hebb’s training algorithm proposed in 1949, which demonstrated how interconnected neurons could exhibit learning behavior. ANN can be classified based on their architecture, topology, and learning regime. In power systems, the most commonly used ANN architecture is the multi-layer feed-forward network.
ANN offer several advantages for power system applications. First, they are fast in processing information. Second, they possess the ability to learn and adapt to data, allowing them to improve their performance over time. Third, ANN are well-suited for non-linear modeling, which is important for accurately representing complex power system behaviors. Additionally, ANN exhibit robustness, making them suitable for voltage security monitoring and control.
Despite these advantages, ANN have some limitations. The dimensionality of ANN can be large, requiring careful consideration of network configuration. Selecting the optimal configuration and training methodology can be challenging. Moreover, ANN are often viewed as “black-box” models, lacking explanation capabilities for the decisions they make. This limits their interpretability and audibility. Lastly, ANN may generate results even when the input data is unreasonable, which can lead to unreliable outcomes.
Fuzzy Logic
Fuzzy logic, introduced by Zadeh in 1964, addresses uncertainty and imprecision commonly encountered in engineering problems. It was first applied to solve power system problems in 1979. Fuzzy set theory extends classical set theory by allowing the degree of association of an element to vary continuously. Unlike classical set theory, where an element either belongs to or does not belong to a set, fuzzy set theory utilizes membership functions to map elements from the universe of discourse to the closed interval [0,1]. These membership functions are designed based on the specific requirements and constraints of the problem at hand.
Fuzzy logic incorporates human experiences and preferences through membership functions and fuzzy rules, making the system understandable to non-expert operators. Consequently, fuzzy logic serves as a versatile methodology for integrating knowledge, heuristics, and theory into controllers and decision makers.
The advantages of fuzzy theory include its ability to accurately represent operational constraints in power systems and the soft nature of fuzzified constraints compared to traditional constraints. Numerous applications of fuzzy set theory in power systems have been explored, including voltage and reactive power control, load forecasting, fault diagnosis, power system protection/relaying, stability, and power system control. Extensive discussions and literature surveys on fuzzy logic and its applications in power systems can be found in various references.
Evolutionary Computation
Evolutionary Computation (EC) is a problem-solving approach that draws inspiration from Darwin’s principle of ‘survival of the fittest.’ The fundamental concept behind EC is to initialize a population of potential solutions to a problem. These solutions are then iteratively improved by introducing random variations to create new candidate solutions. Each solution’s performance in addressing the task is evaluated, and a selection criterion is applied to filter out subpar solutions. This iterative process continues until a specific criterion is met.
EC offers several advantages, including its adaptability to changing problem domains and its ability to generate sufficiently good solutions. However, it is essential to consider the computational requirements and convergence properties associated with EC. It can be further categorized into various subfields, such as Genetic Algorithms (GA), Evolution Strategies, Evolutionary Programming (EP), Genetic Programming, Classified Systems, and Simulated Annealing (SA).
The earliest known work in the field of EC was conducted by Fraser in 1957, where he used a computer to study genetic systems. Since then, numerous optimization techniques inspired by evolutionary principles have been developed and applied.
Genetic Algorithm
The Genetic Algorithm (GA) is a powerful optimization technique that emulates the mechanics of natural selection and genetics. Unlike conventional optimization methods, GA utilizes concepts from population genetics to guide its search for the optimal solution. Rather than performing a point-to-point search, GA operates on populations of potential solutions.
One of the key advantages of GA is that it requires only rough information about the objective function, without imposing restrictions such as differentiability or convexity. This flexibility allows GA to handle a wide range of optimization problems effectively.
Another advantage is that GA operates with a set of solutions from one generation to the next, rather than relying on a single solution. This characteristic makes it less likely for GA to converge on local minima, increasing its ability to find the global optimum.
Furthermore, the solutions generated by GA are based on probabilistic genetic operators like mutation and crossover. As a result, the initial solutions do not heavily influence the search direction of GA, adding another layer of randomness to the optimization process.
However, a major drawback of the GA method is its high time requirement. The computational complexity of GA can be significant, particularly for complex optimization problems.
Simulated Annealing
Simulated Annealing (SA) is a technique inspired by the cooling process of solids, particularly the formation of crystals. SA offers several advantages, including its broad applicability to arbitrary systems and cost functions, its capacity to refine optimal solutions, and its relative simplicity of implementation, even for complex problems. However, a major drawback of SA is the need for repeated annealing, which makes it difficult to determine if the optimal solution has been found. Therefore, an additional method, such as branch and bound, is often required to ascertain the optimality of the solution. SA has found application in diverse power system domains, including transmission expansion planning, unit commitment, maintenance scheduling, and more.
Ant Colony Search
Ant Colony Search (ACS) is a technique introduced by Dorigo in 1992. It draws inspiration from the behavior of real ant colonies and is employed to solve function or combinational problems. ACS algorithms emulate the behavior of real ants to some extent. Key features of ACS include positive feedback for recovering good solutions, distributed computation to avoid premature convergence, and the utilization of a constructive greedy heuristic to discover acceptable solutions in the early stages of the search process. However, the main drawback of the ACS technique is its poor computational performance. It has primarily been utilized in finding the shortest route for transmission networks.
Tabu Search
Tabu Search (TS) is an iterative improvement procedure that begins with an initial solution and aims to find a better solution using a “greatest descent neighborhood” search algorithm. It comprises essential elements such as moves, tabu list, and aspiration level. TS is considered a metahuristic search method for solving global optimization problems. It relies on multi-level memory management and response exploration techniques. TS has found applications in various power system domains, including transmission planning, optimal capacitor placement, unit commitment , hydrothermal scheduling, fault diagnosis/alarm processing, and reactive power planning.
Hybrid AI Techniques
Hybrid AI techniques have gained significant attention in addressing real-life power system problems that may not align with the assumptions of a single AI technique and cannot be effectively solved using a single approach. An alternative strategy involves integrating two or more techniques to leverage their respective strengths and mitigate their weaknesses, resulting in hybrid solutions. This approach has proven valuable in power systems applications, as evidenced by the growing utilization of hybrid AI techniques.
Conclusions
This article provides insights into the significant mathematical optimization and AI techniques employed in power system applications. The discussion also includes various hybrid AI techniques utilized in power systems. Based on the overview presented in this article, the following key conclusions can be drawn:
- Despite notable advancements in mathematical optimization techniques, traditional methods still face challenges in achieving fast and reliable real-time applications in power systems. Addressing issues such as ill-conditioning and convergence difficulties requires substantial efforts.
- The effectiveness of AI heavily relies on accurate problem description and extensive domain knowledge. Expert Systems (ES), which are knowledge-based systems, face a knowledge bottleneck as they lack the ability to learn or adapt to new situations.
- Knowledge-based systems can enhance the capabilities of power systems, while Artificial Neural Networks (ANN) can acquire knowledge through adaptive training and generalization. However, both ANN and ES require expert users for their design and implementation. Additionally, they lack formal model theory and mathematical rigor, making them susceptible to the depth of experts’ knowledge in problem definition.
- Fuzzy theory, with its realistic description of power system problems, and ANN, with its potential for adaptive training and generalization, warrant further investigation.
- Genetic Algorithms (GA) have the advantage of accessing deep knowledge of system problems through well-established models. GA shows great potential in power systems analysis and represents the latest addition to the field.
In summary, the article emphasizes the need for continued research and development to overcome challenges and leverage the strengths of various AI techniques in power system applications.